10.1 그래프란?
10.2 그래프의 정의와 용어
10.3 그래프의 표현 방법
10.4 그래프의 탐색
10.5 깊이 우선 탐색
10.6 너비 우선 탐색
10.1 그래프란?
그래프(graph)
- 연결되어 있는 객체 간의 관계를 표현하는 자료구조
- ex) 트리, 전기회로 소자 연결, 지도 도시 연결
오일러 정리
- 오일러 문제: 모든 다리 "한번씩만" 건너서 처음 출발 장소로 return
- bridge = edge or link 간선
- region = vertex or node 정점
- 모든 정점에 연결된 간선의 수가 짝수이면 오일러 경로 존재!!


따라서 이건 오일러 경로 존재 x
10.2 그래프의 정의와 용어
그래프 정의
- G = (V, E)
- 정점 (vertices) = node
= 여러가지 특성 가질 수 있는 객체를 의미
- V(G) : 그래프 G의 정점들 집합
- |V| = 총 정점 개수
- 간선 (edge) = link
= 정점들 간의 관계를 의미
- E(G) : 그래프 G의 간선들 집합
- |E| = 총 간선 개수
그래프 종류
- undirected graph 무방향 그래프

V(G1) = {0, 1, 2, 3}
E(G1) = {(0,1), (0,2), (0,3), (1,2), (2,3)}
ㄴ 방향 x undirected graph
- 무방향 그래프 정점의 차수 : 하나의 정점에 연결된 다른 정점 수
ㄴ 정점 0의 차수: 3
∑ 정점차수 = 간선수 X 2
- 인접정점 : 하나의 정점에서 간선에 의해 직.접. 연결된 정점
ㄴ 정점 0의 인접 정점: 정점1, 2, 3
- directed graph 방향 그래프

V(G3) = {0, 1, 2}
E(G3) = {<0,1>, <1,0>,<1,2>}
ㄴ 방향 ㅇ directed graph
- 방향 그래프 정점의 차수
=> 진입 차수: 외부에서 오는 간선의 수 / 진출 차수: 외부로 향하는 간선의 수
정점 1의 차수 : 내차수(in-degree) 1 , 외차수(out-degree) 2
∑ 진입 or 진출 차수 = 간선수
(the higher degree, the higher connectivity)
- weighted graph 가중치 그래프 (=네트워크)

- 간선에 비용(cost)나 가중치(weight)가 할당
<== ex)
정점: 각 도시
간선: 도시 연결하는 도로
가중치: 도로의 길이
- subgraph 부분 그래프

- V(G)와 E(G)의 부분집합으로 이루어진 그래프
- 그래프 G1의 부분 그래프들
V(S) ⊆ V(G)
E(S) ⊆ E(G)
그래프의 경로(path)

- 무방향 그래프의 정점 s로부터 정점 e까지의 경로
=> 정점의 나열 s, v1, v2, ..., vk, e
=> 나열된 정점들 간에 반드시 간선 (s,v1), (v1, v2), ..., (vk, e) 존재
- 단순 경로(simple path) : 경로 중에서 반복되는 노드 X 경로
- 사이클(cycle) : 단순 경로의 시작 정점 = 종료 정점
- 단순 사이클(simple cycle) : 시작점 = 종료점 경로 , 반복 노드 X
**오일러사이클 (모든 간선 한번만 건너 처음으로 돌아오는) 은 simple cycle (X)
**해밀턴사이클 (모든 정점 한번만 방문하여 제자리 돌아오는)은 simple cycle (O)
그래프의 연결 정도
- 연결 그래프(connected graph) : 무방향 그래프의 모든 정점 쌍에 대하여 항상 경로 존재
- bridge : 없어지면 비연결 그래프가 되는 간선
- 완전 그래프(complete graph) : 모든 정점이 서로 연결되어 있는 그래프
=> n개의 정점 무방향 완전그래프의 간선 수 : n X (n-1) / 2
그래프 표현 방법 2가지
- 인접 행렬 방법 (2차원 배열 사용)
if ( 간선 (i, j) 존재) M[i][j] = 1;
else M[i][j] = 0;

=> (b)
degree(i) = ∑(j=0~2) M[i][j]
=> (c)
out_degree(i) = ∑(j=0~2) M[i][j]
in_degree(j) = ∑(i=0~2) M[i][j]
인접행렬의 크기 = |V|^2
인접행렬 값 1 항의 개수 = 2|E| (무방향) or |E| (방향)
인접행렬 알고리즘
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 50 //최대 50개 노드
typedef struct GraphType
{
int n; //정점 개수 n=|V| <= MAX_VERTICES(50)
int adj_mat[MAX_VERTICES][MAX_VERTICES];
} GraphType;
//그래프 초기화
void init(GraphType* g)
{
int r,c;
g->n = 0; //정점 총 개수 0개
for (r=0; r < MAX_VERTICES; r++)
for (c=0; c < MAX_VERTICES; c++)
g->adj_mat[r][c] = 0; //간선이 전혀 없다고 초기화
}
//정점 삽입 연산
void insert_vertex(GraphType* g, int v)
{
if (((g->n) + 1) > MAX_VERTICES) //정점개수+1 이 50보다 작으면
{
fprintf(stderr, "그래프: 정점의 개수 초과");
return;
}
g->n++;
}
//간선 삽입 연산
void insert_edge(Graphtype* g, int start, int end)
{
if (start >= g->n || end >= g->n)
{
fprintf(stderr,"그래프: 정점 번호 오류");
return;
}
g->adj_mat[start][end]=1;
g->adj_mat[end][start]=1; //undirected graph에서
}
//main 함수
void main()
{
GraphType* g;
g = (GraphType*)malloc(sizeof(GraphType));
init(g);
for(int i=0; i < 4; i++)
insert_vertex(g,i);
insert_edge(g,0,1);
insert_edge(g,0,2);
insert_edge(g,0,3);
insert_edge(g,1,2);
insert_edge(g,2,3);
print_adj_mat(g);
free(g);
}
- 인접 리스트 방법 (연결 리스트 사용)

- 각 정점에 인접한 정점들을 연결리스트로 표현
- 인접리스트 총 노드(data+link) 개수 = 2|E| (무방향) or |E| (방향)
인접리스트 알고리즘
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 50 //최대 50개 노드
typedef struct GraphNode
{
int vertex;
struct GraphNode *link;
} GraphNode;
typedef struct GraphType
{
int n; //정점 개수 n=|V| <= MAX_VERTICES(50)
GraphNode* adj_list[MAX_VERTICES];
} GraphType;
//그래프 초기화
void init(GraphType* g)
{
int v;
g->n = 0; //정점 총 개수 0개
for (v=0; v < MAX_VERTICES; v++)
g->adj_list[v] = NULL;
}
//정점 삽입 연산
void insert_vertex(GraphType* g, int v)
{
if (((g->n) + 1) > MAX_VERTICES) //정점개수+1 이 50보다 작으면
{
fprintf(stderr, "그래프: 정점의 개수 초과");
return;
}
g->n++;
}
//간선 삽입 연산, v를 u의 인접 리스트에 삽입
void insert_edge(Graphtype* g, int u, int v)
{
GraphNode* node;
if (u >= g->n || v >= g->n)
{
fprintf(stderr,"그래프: 정점 번호 오류");
return;
}
node = (GraphNode*)malloc(sizeof(GraphNode));
node->vertex = v;
node->link = g->adj_list[u];
g->adj_list[u] = node;
}
void print_adj_list(GraphType* g)
{
for (int i=0; i<g->n; i++) {
GraphNode* p = g->adj_list[i];
printf("정점 %d의 인접 리스트 ", i);
while (p!=NULL) {
printf("-> %d ", p->vertex);
p=p->link;
}
}
}
//main 함수
void main()
{
GraphType* g;
g = (GraphType*)malloc(sizeof(GraphType));
init(g);
for(int i=0; i < 4; i++)
insert_vertex(g,i);
insert_edge(g,0,1);
insert_edge(g,1,0);
insert_edge(g,0,2);
insert_edge(g,2,0);
insert_edge(g,0,3);
insert_edge(g,3,0);
insert_edge(g,1,2);
insert_edge(g,2,1);
insert_edge(g,2,3);
insert_edge(g,3,2);
print_adj_list(g);
free(g);
return 0;
}
실행결과
정점 0의 인접 리스트 -> 3 -> 2 -> 1
정점 1의 인접 리스트 -> 2 -> 0
정점 2의 인접 리스트 -> 3 -> 1 -> 0
정점 3의 인접 리스트 -> 2 -> 0
인접 행렬 VS 인접 리스트

10.4 그래프 탐색
- 하나의 정점에서 시작하여 차례대로 모든 정점들을 한번씩 방문
그래프 탐색 알고리즘 2가지 -> DFS, BFS
10.5 깊이 우선 탐색 (DFS - depth first search)

- 한 방향(source node에서 멀어지는 방향)으로 갈 수 있을 때까지 가다가 더 이상 못가면 가장 가까운 갈림길로 돌아와서(후입선출)이 곳으로부터 다른 방향으로 다시 탐색 진행
- 두가지 방법 구현 가능 (1. 순환 호출, 2. 명시적 스택으로 저장하고 꺼내는것)
- 되돌아가기 위해서는 스택 필요 (순환함수 호출로 묵시적인 스택 이용)
| depth_first_search(v): //v는 source node 1. v를 방문되었다고 표시; //필요한 연산(printf) 수행 2. for all u ∈ (v에 인접한 정점) do 3. if (u가 아직 방문되지 않았으면) 4. then depth_first_search(u) //v의 인접 행렬인 u가 다시 새로운 소스노드가 되는 것!! |
**dfs-tree unique (X)
DFS 인접 행렬 버전 프로그램 ========>> O(n^2)
//인접 행렬로 표현한 그래프에 대한 깊이 우선 탐색
void dfs_mat(GraphType* g, int v)
{
int w;
visted[v] = TRUE; //정점 v 방문 표시
printf("정점 %d -> ", v) //방문한 정점 출력
for (w=0; w < g->n; w++) //인접 정점 탐색
if (g->adj_mat[v][w] && !visited[w])
dfs_mat(g,w); //정점 w에서 DFS 새로 시작
}
//main 함수
int main(void)
{
GraphType* g;
g = (GraphType*)malloc(sizeof(GraphType));
init(g);
for (int i=0; i < 4; i++)
insert_vertex(g,i);
insert_edge(g,0,1);
insert_edge(g,0,2);
insert_edge(g,0,3);
insert_edge(g,1,2);
insert_edge(g,2,3);
printf("깊이 우선 탐색\n");
dfs_mat(g,0);
printf("\n");
free(g);
return 0;
}

실행결과
깊이 우선 탐색
정점 0 -> 정점 1 -> 정점 2 -> 정점 3 ->
즉,
아직 방문 안된 인접노드(v)가 있다면 push(v) 하고
아직 방문 안된 인접노드가 없다면 pop(return)
DFS 인접 리스트 버전 프로그램 ========>> O(n+e)
연결리스트의 노드는 데이터필드(인접 정점 번호 저장) + 링크 필드(다음 인접 정점 가리키는 포인터 저장)로 이루어짐
//struct 정의 추가
typedef struct GraphNode {
int vertex;
struct GraphNode* link;
} GraphNode;
typedef struct GraphType {
int n;
GraphNode* adj_list[MAX_VERTICES]l
}GraphType;
int visited[MAX_VERTICES];
//인접 리스트로 표현한 그래프에 대한 깊이 우선 탐색
void dfs_list(GraphType* g, int v)
{
GraphNode* w;
visted[v] = TRUE; //정점 v 방문 표시
printf("정점 %d -> ", v) //방문한 정점 출력
for (w = g->adj_list[v]; w; w = w->link) //인접 정점 탐색
if (!visited[w->vertex])
dfs_list(g,w->vertex); //정점 w에서 DFS 새로 시작
}
명시적인 스택을 이용한 깊이 우선탐색 구현
- 스택을 하나 생성해서 시작 정점을 스택에 넣고, 다시 꺼내서 탐색.
| DFS - iterative(G, v): 1. 스택 S 생성 2. S.push(v) 3. while (not is_empty(S)) do 4. v = S.pop() 5. if (v가 방문되지 않았으면) 6. v를 방문되었다고 표시 //출력 7. for all u ∈ (v에 인접한 정점) do 8. if (u가 아직 방문되지 않았으면) 9. S.push(u) |
10.6 너비 우선 탐색 (BFS - breadth first search)

- 시작 정점으로부터 가까운 정점을 (선입선출) 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
- 큐로 구현
| breadth_first_search(v): 1. v를 방문되었다고 표시; //visted[v] = TRUE; 2. 큐 Q에 정점 v를 삽입; 3. while (Q가 공백이 아니면) do 4. Q에서 정점 w를 삭제; 5. for all u ∈ (w에 인접한 정점) do 6. if (u가 아직 방문되지 않았으면) 7. then u를 큐에 삽입; 8. u를 방문되었다고 표시; |
BFS 인접 행렬 버전 프로그램 ========>> O(n^2)
//인접 행렬로 표현한 그래프에 대한 너비 우선 탐색
void bfs_mat(GraphType* g, int v)
{
int w;
QueueType q;
queue_init(&q); //큐 초기화
visted[v] = TRUE; //정점 v 방문 표시
printf("정점 %d -> ", v) //방문한 정점 출력
enqueue(&q, v); //시작 정점을 큐에 저장
while (!is_empty(&q)) {
v = dequeue(&q); //큐에 정점 추출
for (w=0; w<g->n; w++) //인접 정점 탐색
if (g->adj_mat[v][w] && !visited[w]) {
visited[w] = TRUE;
printf("%d 방문 -> ", w);
enqueue(&q, w); //방문한 정점을 큐에 저장
}
}
}
//main 함수
int main(void)
{
GraphType* g;
g = (GraphType*)malloc(sizeof(GraphType));
graph_init(g);
for (int i=0; i < 6; i++)
insert_vertex(g,i);
insert_edge(g,0,2);
insert_edge(g,2,1);
insert_edge(g,2,3);
insert_edge(g,0,4);
insert_edge(g,4,5);
insert_edge(g,1,5);
printf("너비 우선 탐색\n");
bfs_mat(g,0);
printf("\n");
free(g);
return 0;
}

실행결과
너비 우선 탐색
0 방문 -> 2 방문 -> 4 방문 -> 1 방문 -> 3 방문 -> 5 방문 ->
BFS 인접 리스트 버전 프로그램 ========>> O(n+e)
//struct 정의 추가
typedef struct GraphNode {
int vertex;
struct GraphNode* link;
} GraphNode;
typedef struct GraphType {
int n; //|V|
GraphNode* adj_list[MAX_VERTICES]
}GraphType;
//인접 리스트로 표현한 그래프에 대한 너비 우선 탐색
void bfs_list(GraphType* g, int v)
{
GraphNode* w;
Queuetype q;
init(&q); //큐 초기화
visted[v] = TRUE; //정점 v 방문 표시
printf("%d 방문 -> ", v) //방문한 정점 출력
enqueue(&q, v); //시작정점을 큐에 저장
while (!is_empty(&q)) {
v = dequeue(&q); //큐에 저장된 정점 선택
for (w=g->adj_list[v]; w; w=w->link) //인접 정점 탐색
if (!visited[w->vertex]) { //미방문 정점 탐색
visited[w->vertex] = TRUE; //방문 표시
printf("%d 방문 -> ", w->vertex);
enqueue(&q, w->vertex); //정점을 큐에 삽입
}
}
}
11.1 최소 비용 신장 트리
11.2 Kruskal의 MST 알고리즘
11.3 Prim의 MST 알고리즘
11.4 최단 경로
11.5 Dijkstra의 최단 경로 알고리즘
11.6 Floyd의 최단 경로 알고리즘
11.7 위상 정렬
11.1 최소 비용 신장 트리
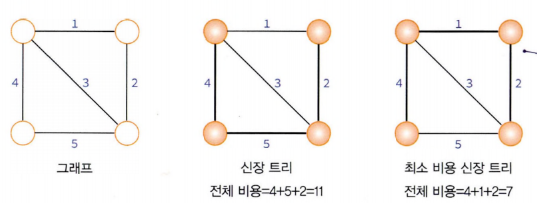
신장트리 (spanning tree)
- 그래프 내의 모든 정점을 포함하지만 사이클은 아닌 트리
- n개의 정점 신장트리 -> n-1개 간선
- 적은 링크만 사용한다고 최소비용은 x -> 링크 구축 비용( 간선 가중치)까지 고려해서 최소 신장 트리 선택해야함

신장트리 알고리즘
| depth_first_search(v): 1. v를 방문되었다고 표시; 2. for all u ∈ (v에 인접한 정점) do 3. if (u가 아직 방문되지 않았으면) 4. then (v, u)를 신장 트리 간선이라고 표시; 5. depth_first_search(u) depth_first_search(v): // 10장 1. v를 방문되었다고 표시; 2. for all u ∈ (v에 인접한 정점) do 3. if (u가 아직 방문되지 않았으면) 4. then depth_first_search(u) |
최소 비용 신장 트리 (MST: minimum spanning tree)
- 모든 정점들을 가장 적은 수의 간선과 비용으로 연결
- 사용된 간선 가중치 합이 최소인 신장트리
- Kruskal, Prim 알고리즘이 대표적 ( 1. 간선 가중치 합 최소 / 2. (n-1)개 간선만 사용 / 3. 사이클 포함 x )
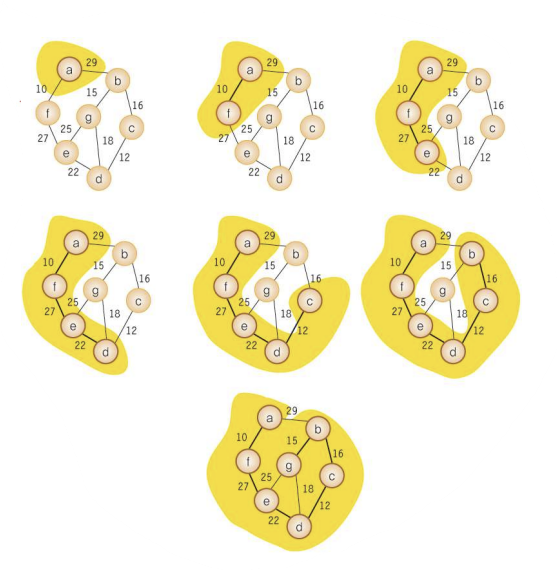
11.2 Kruskal의 MST 알고리즘
Kruskal's MST 알고리즘
- greedy method => 각 단계에서 최선의 답을 선택하여 최종적인 해답에 도달 (but 보장 없어서 항상 최적 해답 검증 필요)
- Kruskal 알고리즘은 최적의 해답을 주는 것으로 증명 됨
- 먼저 간선들을 가중치의 오름차순으로 정렬 -> 사이클 형성 x 간선 찾아 현재의 최소 비용 신장 트리의 집합에 추가 -> 만약 사이클 형성하면 간선 제외하기
| //Kruskal 알고리즘으로 최소 비용 스패닝트리 구하기 //입력: 가중치 그래프 G = (V,E) , n은 노드 개수 //ecounter: MST에 포함된 edge 개수 //k: 현재(가중치 작은 순서부터) 검사한 edge의 개수 //출력: Et, 최소비용 신장 트리 이루는 간선 집합 kruskal(G) E를 w(e1) <= ... <= w(ee)가 되게 정렬 (오름차순으로) Et <- 공집합; ecounter <- 0 k <- 0 while ecounter < (n-1) do //트리의 성질을 loop 종료 조건에 k <- k+1 //다음 가장 weight이 적은 간선의 index if ( Et U {ek}가 사이클을 포함x ); //union-find 연산 활용 then Et <- Et U {ek}; ecounter <- ecounter + 1 return Et |
Union-find 연산
- 같은 집합에 속하는 간선 추가하면 사이클이 형성됨 ==> 따라서 지금 추가하는 간선의 양끝 정점이 같은 집합에 속한지 검사 필요
- 원소가 어떤 집합에 속하는지 알아냄
- Kruskal의 MST 알고리즘에서 사이클 검사에 사용

Union-find 알고리즘
- 부모 포인터 표현: 각 노드에 대해 그 노드의 부모에 대한 포인터만 저장
=> "두 노드가 같은 트리에 있습니다?" 질문에 대답하는데 필요한 정보 저장.
| UNION(a,b): 1. root1 = FIND(a); // 노드a의 루트를 찾는다 2. root2 = FIND(b); // 노드b의 루트를 찾는다. 3. if root1 =/ root2 // 합한다. 4. parent[root1] = root2; //parent[root2] = -1로 초기화 FIND(curr): //curr의 루트를 찾는다. 1. if (parent[curr] == -1) //자기 자신 2. return curr; //루트 3. while (parent[curr] != -1) //O(log|V|) curr = parent[curr]; 4.return curr; |
a와 b의 root node가 같은가? == a와 b가 같은 그룹에 속했는가? == a와 b 사이에 edge를 추가하면 cycle이 생기는가?
union-find 프로그램
int parent[MAX_VERTICES]; //부모 노드
void set_init(int n) //n은 정점의 개수
{
for(int i=0; i<n; i++)
parent[i] = -1;
}
//curr가 속하는 집합을 반환한다
//return (루트 or 대표노트(X)), where parent[x] == -1
int set_find(int curr)
{
if(parent[curr] == -1)
return curr; //루트
while(parent[curr] != -1)
curr = parent[curr];
return curr;
}
//두개의 원소가 속한 집합을 합친다.
void set_union(ina a, int b)
{
int root1 = set_find(a); //노드 a의 루트를 찾는다
int root2 = set_find(b); //노드 b의 루트를 찾는다
if (root1 != root2) //합한다.
parent[root1] = root2; //a의 대표노드의 부모를 b의 대표노드로 변경
}
union-find 이용한 Kruskal's 프로그램
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 1000
int parent[MAX_VERTICES]; //부모 노드
void set_init(int n) //초기화
{
for (int i=0; i<n; i++)
parent[i] = -1;
}
//curr가 속하는 집합을 반환한다.
int set_find(int curr)
{
if (parent[curr] == -1)
return curr; //루트
while (parent[curr] != -1) curr = parent[curr];
return curr;
}
//두개의 원소가 속한 집합을 합친다.
void set_union(int a, int b)
{
int root1 = set_find(a); //노드 a의 루트를 찾는다.
int root2 = set_find(b); //노드 b의 루트를 찾는드ㅏ.
if (root1 != root2) //합한다.
parent[root1] = root2;
}
struct Edge { //간선을 나타내는 구조체
int start, end, weight;
};
typedef struct GraphType {
int n; //간선의 개수
int nv; //정점의 개수
struct Edge edges[2*MAX_VERTICES];
} GraphType;
//그래프 초기화
void graph_init(GraphType* g)
{
g->n = 0;
g->nv = 0;
for (int i = 0; i < 2 * MAX_VERTICES; i++) {
g->edges[i].start = 0;
g->edges[i].end = 0;
g->edges[i].weight = INF;
}
}
// 간선 삽입 연산
void insert_edge(GraphType* g, int start, int end, int w)
{
g->edges[g->n].start = start;
g->edges[g->n].end = end;
g->edges[g->n].weight = w;
g->n++;
}
// qsort()에 사용되는 함수
int compare(const void* a, const void* b)
{
struct Edge*x = (struct Edge*)a;
struct Edge*y = (struct Edge*)b;
return (x->weight - y->weight); //return 값 < 0 : a<b
//return 값 = 0 : a==b
//return 값 > 0 : a>b
}
//kruskal의 최소 비용 신장 트리 프로그램
void kruskal(GraphType* g)
{
int edge_accepted = 0; // 현재까지 선택된 간선의 수
int uset, vset; // 정점 u와 정점 v의 집합 번호
struct Edge e;
set_init(g->nv); // 집합 초기화 ∀𝑖 parent[i] = -1
qsort(g->edges, g->n, sizeof(struct Edge), compare);
\\After qsort() ===>> g->edges[0].weight ≤ g->edges[1].weight ≤ … ≤ g->edges[(g->n)−1].weight
printf("크루스칼 최소 신장 트리 알고리즘 \n");
int i = 0; // 오름차순으로 검색한 edge 들의 개수
while (edge_accepted < (g->nv - 1) ) { // 간선의 수 < (|V|-1) => tree의 조건
e = g->edges[i]; //다음 최소 ㅣㅂ용 간선
uset = set_find(e.start); // 정점 u의 집합 번호
vset = set_find(e.end); // 정점 v의 집합 번호
if (uset != vset) { // 서로 속한 집합이 다르면
printf("간선 (%d,%d) %d 선택\n", e.start, e.end, e.weight);
edge_accepted++;
set_union(uset, vset); // 두개의 집합을 합친다.
} // if문은 간선e를 MST 그래프에 포함시킴
i++;
} // end of while
}
int main(void)
{
GraphType* g;
g = (GraphType*)malloc(sizeof(GraphType));
graph_init(g);
//g->nv=7;
insert_edge(g, 0, 1, 29);
insert_edge(g, 1, 2, 16);
insert_edge(g, 2, 3, 12);
insert_edge(g, 3, 4, 22);
insert_edge(g, 4, 5, 27);
insert_edge(g, 5, 0, 10);
insert_edge(g, 6, 1, 15);
insert_edge(g, 6, 3, 18);
insert_edge(g, 6, 4, 25);
kruskal(g);
free(g);
return 0;
}
실행결과

Kruskal's MST 알고리즘 분석
- Kruskal 알고리즘에서는 간선 정렬해야해서 간선들의 집합으로 저장 (GraphType 안에 간선들만 저장)
- 정렬 알고리즘으로는 qsort() 함수 사용
- Kruskal 알고리즘은 간선 정렬 시간에 좌우 ( 사이클 테스트 작업은 영향 적음)
- 네트워크 간선 e개를 퀵정렬과 효율적인 알고리즘으로 정렬하면 Kruskal 알고리즘의 시간 복잡도는 O(e*loge)
- worst case의 big O ==>> complete graph , |E|=(|V|x|V|-1)/2 , O(|V|^2log|V|^2)
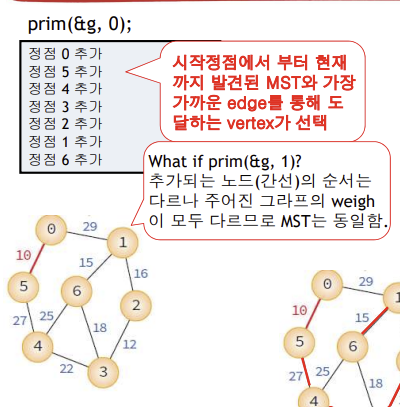
11.3 Prim의 MST 알고리즘
Prim's MST 알고리즘
- 시작 정점에서부터 출발해서 신장 트리 집합을 단계적으로 확장함
- 신장 트리 집합에 인접한 정점 중 최저 간선으로 연결된 정점 선택해서 신장 트리 집합에 추가
- 시작 정점만으로 시작했다가 최저 간선 정점 선택하여 확장하다가 n-1 간선 가질 때까지 계속
Prim's MST 알고리즘
| //최소 비용 신장 트리 구하는 Prim 알고리즘 //입력: 네트워크 G=(V,E), s는 시작 정점 //출력: 최소 비용 신장 트리 이루는 정점 집합 //**Uniqueness of MST => yes only when 모든 weight이 다르다면 Prim(G,s) for each u ∈V do dist[u] <- 무한집합 dist[s] <- 0 //우선 순위큐 Q에 모든 정점을 삽입(우선순위는 dist[]) min heap for i <- 0 to n-1 do u <- delete_min(Q) 화면에 u를 출력 for each v { (u의 인접 정점) //**dist[v]: v가 현 MST와 직접연결된 간선의 weight //**Update dist[] : 방금 MST에 포함된 vertex와 직접연결된 (아직 MST에 포함 안된 ) 노드들의 dist[]를 변경 if ( v ∈ Q and weight [u][v] < dist[v] ) //여전히 Q에 있는 노드 = 아직 MST에 포함 X 노드 -> selected[] then dist[v] <- weight[u][v] |
Prim's MST 프로그램
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 1000L
typedef struct GraphType
{
int n; // 정점의 개수
int weight[MAX_VERTICES][MAX_VERTICES];
} GraphType;
int selected[MAX_VERTICES];
int distance[MAX_VERTICES];
// 최소 dist[v] 값을 갖는 정점을 반환
int get_min_vertex(int n)
{
int v, i;
for (i = 0; i < n; i++)
if (!selected[i]) {
v = i;
break;
}
for (i = 0; i < n; i++)
if (!selected[i] && (distance[i] < distance[v])) v = i; //**v는 아직 MST에 포함X 노드 아무거나
return (v); //**v는 아직 MST에 포함되지 않은 노드들 중 distance[]값 가장 작은 것
}
//시간복잡도는 O(|V|^2)
void prim(GraphType* g, int s) //s는 시작정점
{
int i, u, v;
for (u = 0; u < g->n; u++)
distance[u] = INF;
distance[s] = 0; //|V|개의 노드가 모두 MST에 포함될 때까지 or
for (i = 0; i < g->n; i++) {
u = get_min_vertex(g->n); // u = 최소 dist[v] 값을 갖는 정점
selected[u] = TRUE;
if (distance[u] == INF) return; //g is a disconnected graph
printf("정점 %d 추가\n", u); // MST ∪= {u}
for (v = 0; v < g->n; v++) //u의 모든 간선들
if (g->weight[u][v] != INF)
if (!selected[v] && g->weight[u][v] < distance[v])
distance[v] = g->weight[u][v]; //이전 MST와의 거리(dist[v])보다 방금 전 MST에 포함된
//노드(u)를 통한 거리가 더 가까우면 Update dist[v]
}
}
int main(void)
{
GraphType g = { 7,
{ { 0, 29, INF, INF, INF, 10, INF },
{ 29, 0, 16, INF, INF, INF, 15 },
{ INF, 16, 0, 12, INF, INF, INF },
{ INF, INF, 12, 0, 22, INF, 18 },
{ INF, INF, INF, 22, 0, 27, 25 },
{ 10, INF, INF, INF, 27, 0, INF },
{ INF, 15, INF, 18, 25, INF, 0 } }
}; // 가중치 인접행렬
prim(&g, 0);
return 0;
}
typedef struct GraphType
{
int n; // 정점의 개수
int weight[MAX_VERTICES][MAX_VERTICES];
} GraphType실행결과
Prim's MST 알고리즘 분석
- 주 반복문이 정점의 수 n만큼 반복하고, 내부반복이 n번 반복하므로 Prim의 알고리즘은 O(n2)의 복잡도
Kruskal vs Prim
- Kruskal은 edge weight이 가장 작은 노드들부터 시작 vs Prim은 임의 노드에서 시작
- Kruskal은 간선들이 비용 순서대로 한번씩만 처리 vs Prim 은 최소 거리 얻기 위해 하나의 노드 여러번 방문(update dist[x]) 함.
- Kruskal은 Disconnected graph에서도 동작 vs Prim은 Connected graph에서만 동작
- Kruskal 은 모든 edge들 정렬해야 하니까 sparse graph에서 더 빨리 실행 vs Prim은 dense graphs에서 더 빨리 실행
- Kruskal 알고리즘은 간선 기반 vs Prim 알고리즘은 정점 기반
- Kruskal은 Forest(disconnected components) 생산 vs Prim은 한개의 connected component 생산
- Kruskal 알고리즘에서는 이전 단계에서 만들어진 신장 트리와는 상관 xx 무조건 최저 간선만을 선택 vs Prim 알고리즘은 이전 단계에서 만들어진 신장 트리 확장 방식
- Kruskal 알고리즘 복잡도는 O(eloge) => 희소 그래프 적합 vs Prim 알고리즘 복잡도는 O(n^2)이므로 밀집 그래프 적합
11.4 최단 경로
최단경로
- 네트워크에서 정점 u와 정점 v를 연결하는 경로 중 간선들의 가중치 합이 최소가 되는 경로
- 가중치 인접행렬

최단경로 알고리즘
- Dijkstra 알고리즘 : 하나의 시작 정점 ~ 모든 다른 정점까지의 최단경로 계산
- Floyd 알고리즘 : 모든 정점 ~ 모든 다른 정점까지의 최단경로 계산
- 인접행렬 : 간선이 없으면 인접 행렬 값 0 <-> 가중치 인접 행렬 : 간선이 없으면 무한대 값 (가중치 0이 가능하므로)
11.5 Dijkstra's 최단경로 알고리즘
- 집합 S: 시작 정점 v로부터의 최단경로가 이미 발견된 정점들의 집합
- distance 배열: 최단경로가 알려진 정점들만을 이용한 다른 정점들까지의 최단경로 거리
- 매 단계에서 가장 작은 distance 값 정점을 집합 S에 추가
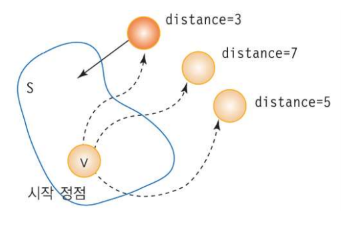
[ 증명 ]
1. 각 단계에서 S안에 있지 않은 정점 (아직 시작정점 source node로부 부터의 최단 경로가 발견 X 노드) 중에서 가장 distance값이 작은 정점(v로 부터 이미 최단 경로가 결정된 노트들만을 이용해 가장 짧은 길이로 도달할 수 있는 노드)을 S에 추가
2. 정점 w를 거쳐 정점 u로 가는 가상적인 더 짧은 경로가 있다고 가정
3. (정점 v ~ 정점 u) = (정점 v ~ 정점 w) + (정점 w ~ 정점 u)
4. but. 항상 (정점 v ~ 정점 w) > 최단경로 ==> bcz 현재 distance 값이 최소인 정점은 u이기 때문
5. 새로운 정점이 S에 추가되면 distance 값 갱신
=> distance[w] = min(distance[w], distance[u] + weight[u][w])

| //입력: 가중치 그래프 G, 가중치는 음수x **강조하심 //출력: distance 배열, distance[u]는 v에서 u까지의 최단거리. shortest_path(G,v): 1. S <- {v} 2. for 각 정점 wㅌG do 3. distance[w] <- weight[v][w]; //v와 직접 연결되지 않은 노드는 INF 4. while 모든 정점이 S에 포함되지 않으면 do 5. u <- 집합 S에 속하지 않는 정점 중 최소 distance 정점; 6. S <- S U {u} 7. for u에 인접하고 S에 있는 각 정점 z do 8. if distance[u] + weight[u][z] < distance[z] 9. then distance[z] <- distance[u] + weight[u][z]; |
Dijkstra's 최단경로 프로그램
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 1000000 /* 무한대 (연결이 없는 경우) */
typedef struct GraphType
{
int n; // 정점의 개수
int weight[MAX_VERTICES][MAX_VERTICES];
} GraphType;
int distance[MAX_VERTICES]; /* 시작정점으로부터의 최단경로 거리 */
int found[MAX_VERTICES]; /*방문한 정점 표시*/
int choose(int distance[], int n, int found[]) //O(|V|) 시간복잡도 (min heap은 O(log|V|)
{
int i, min, minpos;
min = INT_MAX;
minpos = -1;
for (i = 0; i < n; i++)
if (distance[i] < min && !found[i]) {
min = distance[i];
minpos = i;
}
return minpos;
}
void shortest_path(GraphType* g, int start) //O(|V|^2) 시간복잡도 (min heap은 O(|V|log|V|))
{
int i, u, w;
for (i = 0; i < g->n; i++) { /* 초기화 */
distance[i] = g->weight[start][i];
found[i] = FALSE;
}
found[start] = TRUE; /* 시작 정점 방문 표시 */
distance[start] = 0;
for (i = 0; i < g->n - 1; i++) {
print_status(g);
u = choose(distance, g->n, found); //O(log|V|)
found[u] = TRUE;
for (w = 0; w < g->n; w++)
if (!found[w])
if (distance[u] + g->weight[u][w] < distance[w])
distance[w] = distance[u] + g->weight[u][w];
} //heap 자료구조에서 key를 update 하지 말고 줄어든 key값을 가지는 새로운 노드를 추가하는 방식으로 구현
} (동일 노트 & 다른 distance[]를 허용) =>> O(log|V|)
void print_status(GraphType* g)
{
static int step = 1;
printf("STEP %d :", step++);
printf("distance: ");
for (int i=0; i<g->n; i++) {
if (distance[i] == INF)
printf(" * ");
else
printf("%2d ", distance[i]);
}
printf("\n");
printf(" found: ");
for (int i=0; i<g->n; i++)
printf("%2d ", found[i]);
printf("\n\n");
}
int main(void)
{
GraphType g = { 7,
{ { 0, 7, INF, INF, 3, 10, INF },
{ 7, 0, 4, 10, 2, 6, INF },
{ INF, 4, 0, 2, INF, INF, INF },
{ INF, 10, 2, 0, 11, 9, 4 },
{ 3, 2, INF, 11, 0, INF, 5 },
{ 10, 6, INF, 9, INF, 0, INF },
{ INF, INF, INF, 4, 5, INF, 0 } }
};
shortest_path(&g, 0);
return 0;
}실행 결과
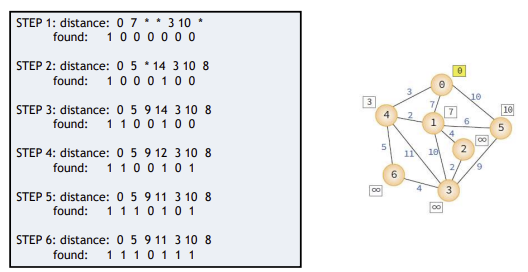
Dijkstra's 최단경로 알고리즘 복잡도
- 네트워크에 n개의 정점이 있다면, Dijkstra의 최단경로 알고리즘은 주반복문을 n번 반복하고 내부 반복문을 2n번 반복하므로 O(n^2)의 복잡도 가짐
--> min heap은 O(|V|log|V|)
11.6 Floyd의 최단 경로 알고리즘
- 모든 정점 사이의 최단 경로를 구하려면 앞의 Dijkstra 알고리즘을 정점 수만큼 반복 실행하면 됨 but Floyd는 더 간단 좋
Floyd warshall 최단경로 알고리즘
| floyd(G): 1. for k <- 0 to n-1 2. for i <- to n-1 3. for j <- 0 to n-1 4. A[i][j] = min(A[i][j], A[i][k] + A[k][j]) |
- 모든 정점 사이의 최단 경로 찾음
- 2차원 배열 A를 이용하여 3중 반복 루프로 구성
- Ak[i][j] : 0부터 k까지의 정점만을 이용한 정점 i에서 j까지의 최단 경로 길이
- A-1(가중치 행렬 초기 상태) -> A0 -> A1 -> ... -> An-1 순으로 최단 경로 구해감
- Ak-1까지 구해진 상태에서 k번째 정점이 추가로 고려된다면....
==> shortest_path(i to j) = min(shortest_path(i to k) + shortest_path(k to j))
- 0부터 k까지의 정점만을 사용해 정점 i에서 j까지의 최단 경로 길이 구하는 2가지 방법
- 정점 k 거치지 X
Ak[i][j]는 k보다 큰 정점 통과 X => 최단거리는 여전히 Ak-1[i][j]
즉, Ak[i][j] = Ak-1[i][j]
2. 정점 k 거치는 O
i에서 k까지 최단거리 Ak-1[i][j] + k에서 j까지 최단거리 Ak-1[k][j]
즉, Ak[i][j] = Ak-1[i][k] + Ak-1[k][j]
Floyd의 최단경로 프로그램
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 100
#define INF 1000000 /* 무한대 (연결이 없는 경우) */
typedef struct GraphType {
int n; //정점의 개수
int weight[MAX_VERTICES][MAX_VERTICES];
} GraphType;
int A[MAX_VERTICES][MAX_VERTICES];
void printA(GraphType *g)
{
int i, j;
printf("====================\n");
for (i=0; i<g->n; i++) {
for (j=0; j<g->n; j++) {
if (A[i][j] == INF)
printf(" * ");
else printf("%3d ", A[i][j]);
}
printf("\n");
}
printf("====================\n");
}
//
void floyd(GraphType* g)
{
int i,j,k;
for (i=0; i < g->n; i++)
for (j=0; j < g->n; j++)
A[i][j] = g->weight[i][j];
printA(g);
for (k=0; k < g->n; k++)
{
for (i=0; i < g->n; i++)
for (j=0; j < g->n; j++)
if (A[i][j] + A[i][j] < A[i][j])
A[i][j]= A[i][k] + A[k][j];
printA(g);
}
}
//main 함수
int main(void)
{
GraphType g = { 7,
{ { 0, 7, INF, INF, 3, 10, INF },
{ 7, 0, 4, 10, 2, 6, INF },
{ INF, 4, 0, 2, INF, INF, INF },
{ INF, 10, 2, 0, 11, 9, 4 },
{ 3, 2, INF, 11, 0, INF, 5 },
{ 10, 6, INF, 9, INF, 0, INF },
{ INF, INF, INF, 4, 5, INF, 0 } }
};
floyd(&g);
return 0;
}
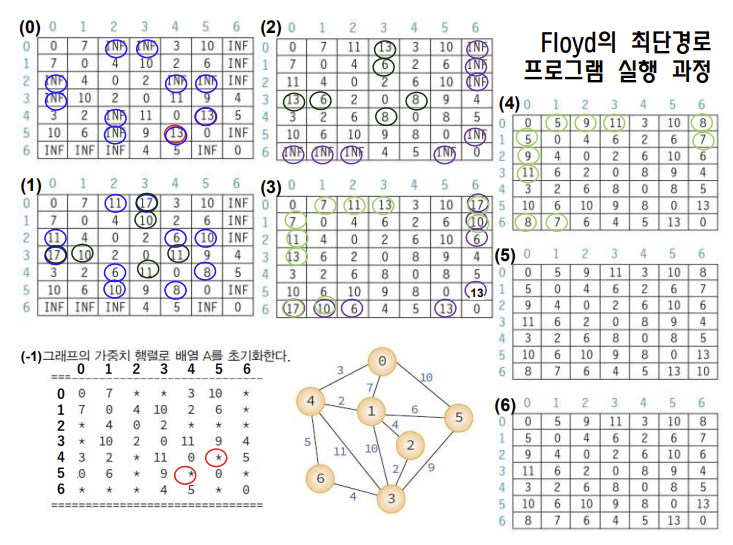
Floyd 최단경로 알고리즘 시간 복잡도
- 네트워크에 n개의 정점이 있다면, Floyd의 최단경로 알고리즘은 3중 반복문을 실행되므로 시간 복잡도는 O(n^3) 이 된다 - 모든 정점 상의 최단경로를 구하려면 Dijkstra의 알고리즘 O(n^2)을 n번 반복해도 되며, 이 경우 전체 복잡도는 O(n^3)
11.7 위상정렬 (topological sort)
- **방향 그래프에서 간선 <u, v>가 있다면 정점 u는 정점 v를 선행
- 방향 그래프 정점들의 선행 순서를 위배하지 않으면서도 모든 정점 나열하여 선행 관계 표현함
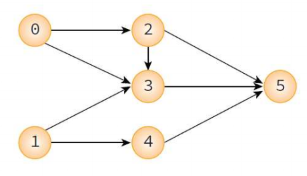
위상 순서
-> (0,1,2,3,4,5) , (1,0,2,3,4,5) 동일한 그래프에 여러 위상정렬 ok
but (2,0,1,3,4,5)는 위상 순서 x 왜냐하면 2번이 0번 앞
위상정렬 알고리즘
| //Input: 그래프 G=(V,E) //Output: 위상 정렬 순서 topo_sort(G) for i<-0 to n-1 do if (모든 정점이 선행 정점을 가지면) //방향그래프에서만 가능!! then 사이클이 존재하고 위상 정렬 불가; 선행 정점을 가지지 않는 정점 v 선택; //a vertex with no incoming edges ..즉, in_degree == 0 v 출력 v와 v에서 나온 모든 간선들을 그래프에서 삭제; |
위상정렬 프로그램
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 50
typedef struct GraphNode {
int vertex;
struct GraphNode* link'
} GraphNode;
typedef struct GraphType {
int n; // |V|
GraphNode* adj_list[MAX_VERTICES];
} GraphType;
//그래프 초기화
void graph_init(GraphType* g) {
g->n = 0;
for(int i=0; i<MAX_VERTICES; i++)
g->adj_list[i] = NULL;
}
//정점 삽입 연산
void insert_vertex(GraphType *g, int v)
{
if (((g->n) + 1) > MAX_VERTICES) {
fprintf(stderr, "그래프: 정점의 개수 초과");
return;
}
g->n++;
}
//간선 삽입 연산, v를 u의 인접 리스트에 삽입
void insert_edge(GraphType *g, int u, int v)
{
GraphNode *node;
if (u>=g->n || v>=g->n) {
fprintf(stderr, "그래프: 정점 번호 오류");
return;
}
node = (GraphNode *)malloc(sizeof(GraphNode));
node->vertex = v;
node->link = g->adj_list[u];
g->adj_list[u] = node;
}
#define MAX_STACK_SIZE 100
typedef int element;
typedef struct {
element stack[MAX_STACK_SIZE];
int top;
} StackType;
//스택 초기화 함수
void init(StackType *s)
{
s->top = -1;
}
//공백 상태 검출 함수
int is_empth(StackType *s)
{
return (s->top == -1);
}
//포화 상태 검출 함수
int is_full(StrackType *s)
{
return (s->top == (MAX_STACKSIZE - 1));
}
//삽입함수
void push(StackType *s, element item)
{
if (is_full(s)) {
fprintf(stderr, "스택 포화 에러\n");
return;
}
else s->stack[++(s->top)] = item;
//삭제함수
element pop(StackType *s)
{
if (is_empth(s)) {
fprintf(stderr, "스택 공백 에러\n");
exit(1);
}
else return s->stack[(s->top)--];
}
//위상정렬 수행
int topo_sort(GraphType* g)
{
int i;
StackType s;
GraphNode* node;
//모든 정점의 진입 차수 계산
int* in_degree = (int*)malloc(g->n*sizeof(int));
for (i=0; i < g->n; i++) //초기화
in_degree[i] = 0;
for (i=0; i < g->n; i++) {
GraphNode* node = g->adj_list[i]; //정점 i에서 나오는 간선들
while (node!= NULL) {
in_degree[node->vertex]++; //edge(i,node->vertex)
node = node->link;
}
}
//진입차수가 0인 정점을 스택에 삽입 ==> why stack? 큐를 쓴다면? 가능!!
init(&s); //스택 초기화
for (i=0; i<g->n; i++) {
if (in_degree[i] == 0) push(&s, i); //in_degree가 0인 노드들을 모두 push
}
//위상 순서 생성
while(!is_empty(&s)) {
int w;
w = pop(&s);
printf("정점 %d ->", w); //정점 출력 output) 1 4 0 2 3 5
node = g->adj_list[w]; //각 장점의 진입 차수 변경
while (node != NULL) {
int u = node->vertex;
in_degree[u]--; //진입 차수 감소
if(in_degree[u] == 0) push(&s, u);
node = node->link; //다음 정점
} //end of inner while
} //end of outer while
free(in_degree);
printf("\n");
return (i == g->n); //반환값이 1이면 성공, 0이면 실패~
//main 함수
int main(void)
{
GraphType g;
graph_init(&g);
insert_vertex(&g,0); insert_vertex(&g,1);
insert_vertex(&g,2); insert_vertex(&g,3);
insert_vertex(&g,4); insert_vertex(&g,5);
//정점 0의 인접 리스트 생성
insert_edge(&g,0,2); insert_edge(&g,0,3);
//정점 1의 인접 리스트 생성
insert_edge(&g,1,3); insert_edge(&g,1,4);
//정점 2의 인접 리스트 생성
insert_edge(&g,2,3); insert_edge(&g,2,5);
//정점 3의 인접 리스트 생성
insert_edge(&g,3,5);
//정점 4의 인접 리스트 생성
insert_edge(&g,4,5);
//위상 정렬
topo_sort(&g);
//동적 메모리 반환 코드 생략
return 0;
}
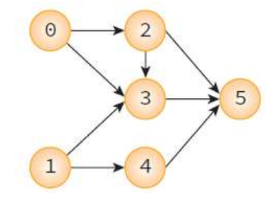
실행 결과
정점 1 -> 정점 4 -> 정점 0 -> 정점 2 -> 정점 3 -> 정점 5 ->
12.1 정렬이란?
12.2 선택 정렬
12.3 삽입 정렬
12.4 버블 정렬
12.5 쉘 정렬
12.6 합병 정렬
12.7 퀵 정렬
12.8 히프 정렬
12.9 기수 정렬
12.10 정렬 알고리즘의 비교
12.11 정렬의 응용: 영어 사전을 위한 정렬
12.1 정렬
정렬
- 물건을 크기 순으로 오름차순이나 내림차순으로 나열하는 것 (자료 탐색에서 필수!)
- 정렬 대상 => 일반적으로 레코드(record) ( 예를 들면 학생들이 레코드면, 학번 이름 등이 필드)
- 레코드는 필드라는 보다 작은 단위로 구성되고 키필드(이름 등)로 레코드와 레코드를 구별

- 모든 경우에 최적인 정렬 알고리즘은 X
- 정렬 알고리즘 평가 기준 => 비교 횟수 빈도, 이동 횟수 빈도 (빅오표기법으로)
분류1
- 단순, 비효율 => 삽입 정렬 , 선택 정렬 , 버블정렬
- 복잡, 효율 => 퀵정렬 , 히프정렬 , 합병정렬 , 기수정렬
분류2
- 내부 정렬 : 모든 데이터가 주기억장치에 저장된 상태에서 정렬 (여기서는 내부정렬만 다룸)
- 외부 정렬 : 외부기억장치에 대부분 데이터, 일부만 주기억장치에 저장된 상태에서 정렬
분류3
- 안정 O (같은 키 값 레코드들이 정렬 후에도 바뀌지 X) => 삽입 정렬 , 선택 정렬 , 합병정렬
- 안정 X => 선택 정렬, 히프 정렬
***in-place sorting 제자리 정렬: 입력 배열 이외에는 다른 추가 메모리를 요구하지 않는 정렬 방법
12.2 선택 정렬
선택정렬

- 정렬된 왼쪽 리스트와 정렬이 안 된 오른쪽 리스트 가정
- 초기에 왼쪽 0리스트 비어 있고, 정렬할 숫자들은 모두 오른쪽 리스트에
- 오른쪽 리스트에서 가장 작은 숫자 선택해서 왼쪽 리스트로 이동하는 작업 반복
선택정렬 알고리즘
| selection_sort(A,n) 1. for i<-0 to n-2 do 2. least <- A[i], A[i+1],..., A[n-1] 중에서 가장 작은 값의 인덱스; 3. A[i]와 A[least]의 교환; 4. i++; |
- i 값은 0~n-2까지만 변화되는 점. 왜냐면 만약 list[0]~list[n-1]까지 정렬 되어있으면 list[n-1]이 이미 가장 커서 n-1까지 정렬할 필요 X
선택정렬 코드
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 10
#define SWAP(x,y,t) ( (t)=(x), (x)=(y), (y)=(t) ) //세번의 이동(교환)
int list[MAX_SIZE];
int n;
void selection_sort(int list[], int n)
{
int i,j,least,temp;
for (i=0; i<n-1; i++) //한 round마다 한 개의 record가 최종 정렬된 위치를 찾아 가면서, sorted/unsorted part 길이가 각각 1씩 증가/감소
least = i; //비교 횟수 = (n-1) + (n-2) + ... + 1 = n(n-1)/2 = O(n^2)
for (j=i+1; j<n; j++) //최솟값 탐색
if (list[j] < list[least]) least = j;
SWAP(list[i], list[least], temp); //이동회수 = 3x(n-1)번의 swapping = O(n)
}
}
//main 함수
int main(void)
{
int i;
n = MAX_SIZE;
srand(time(NULL));
for (i=0; i<n; i++) //난수 생성 및 출력
list[i] = rand() % 100; //난수 발생 범위 0-99
selection_sort(list, n); //선택정렬 호출
for (i=0; i<n; i++)
printf("%d", list[i]);
printf("\n");
return 0;
}
결과:
16 24 25 38 48 64 87 90 93 96
**만일 정렬해야할 데이터 셋이 이미 원하는 순서로 정렬되어 있어도 swapping(이동) 발생. 아래 if 문 추가하면 됨
즉. 최소값이 자기 자신이면 자료이동 X
if ( i != least)
SWAP(list[i], list[least], temp);
선택정렬 복잡도 분석
- 비교 횟수(= 내부루프 실행 횟수) : (n-1) + (n-2) + ... + 1 = n(n-1)/2 = O(n^2)
- 이동 횟수(= 외부루프 실행 횟수) : 3(n-1)
- 전체 시간적 복잡도 : O(n^2) = 비교횟수 + 이동횟수 한 것
- 안정성 만족 X. 같은 레코드가 있는 경우에 상대적인 위치 변경 가능 ( unstable, in-place sort )
- 메모리 사용 최소화 (고정된 양의 추가 메모리만 필요 ) ==> 공간 복잡도 : O(1)
12.3 삽입정렬
삽입정렬 (insertion sort)

- 정렬되어 있는 부분에 새로운 레코드를 정렬이 유지되는 위치에 삽입 반복
삽입정렬 알고리즘
| insertion_sort(A, n) //오름차순 1. for i<-1 to n-1 do //A[0]은 기정렬된 것으로 간주하여 A[1]부터 시작 2. key <- A[i]; 3. j <- i-1; //#3~#6 sorted part에서 A[i]가 순서있게 놓일 위치 찾는 과정 4. while j ≥ 0 and A[j] > key do 5. A[j+1] <- A[j]; //key값이 들어갈 자리를 확보하기 우함 6. j <- j-1; //하나 더 앞에 것과 비교 7. A[j+1] <- key //while문에서 exit 할 때 마지막으로 비교된 element가 A[j] (0<=j<=i-1)이고 비어있는 element는 A[j+1] |
(i=5) round에서
(1) 만일 A[5]=key가 A[4]보다 크다면... j가 4이므로 하나 증가시켜 원래자리 A[5]에 key 값 저장
(2) 만일 A[5]=key가 A[0]보다 작다면... j가 -1이므로 하나 증가시켜 A[0]에 key값 저장
삽입정렬 코드
//삽입정렬
void insertion_sort(int list[], int n)
{
int i, j, key; //추가 공간은 변수(key) 하나. 상수이므로 공간복잡도 O(1)
for (i=1; i < n; i++)
{
key = list[i];
for (j=i-1; j>=0 && list[j] > key; j--)
list[j+1] = list[j]; //레코드의 오른쪽 이동
list[j+1]=key;
}
}
삽입정렬 복잡도 분석
(Inner for문 복잡도는 n 나눈 것 )
- 최선 : O(n) --->> 이미 정렬되어 있는 경우
ㄴ 비교 n-1번 **바로 앞의 것과 1회씩만 비교
ㄴ 이동 2(n-1) (2번의 이동.)
- 최악 : O(n^2) --->> 역순으로 정렬되어 있는 겨우
ㄴ모든 단계에서 앞에 놓인 자료 전부 이동
ㄴ 비교: 1+2+ .... + (n-1) = n(n-1)/2 = O(n^2)
ㄴ이동: n(n-1)/2 + 2(n-1) = O(n^2)
- 평균 : O(n^2) **small datasets에 적합
- 많은 이동 필요 -> 레코드가 크면 불리
- 안정된 정렬방법
- 대부분 정렬되어 있으면 효율적
- **in-place sort 메모리 사용 최적화(고정된 양의 추가 메모리만 필요) ==> 공간복잡도 O(1)
12.4 버블 정렬
버블정렬

- 인접한 2개의 레코드 비교하여 순서대로 되어 있지 않으면
서로 교환
- **In each round, unsorted part에서 가장 큰 record가 최종 위치를 찾아 감 (여기서는 8). 마치 거품 보글보글 같다.
버블정렬 알고리즘
| BubbleSort(A, n) 1. for i<-n-1 to 1 do 2. for j<-0 to i-1 do 3. j와 j+1번째의 요소가 크기 순이 아니면 교환 4. j++; 5. i--; |
버블정렬 코드
#define SWAP(x,y,t) ( (t)=(x), (x)=(y), (y)=(t) )
void bubble_sort(int list[], int n) //오름차순
{
int i,j,temp;
for (i=n-1; i>0; i--)
{
for (j=0; j<i; j++) //앞뒤의 레코드를 비교한 후 교체
if (list[j] > list[j+1])
SWAP(list[j], list[j+1], temp); //3회 이동 연산
}
}
버블 정렬 복잡도 분석
- 비교 횟수 (최상, 평균, 최악 모두 일정) :1+2+...+(n-1) = n(n-1)/2 = O(n^2)
- 이동 횟수
ㄴ 최악 - 역순으로 정렬된 경우 이동 횟수 = 3 (swap이 3개 이동이라)* 비교 횟수
ㄴ 최선 - 이미 정렬된 경우(이동 한 번도 발생X) = 이동 횟수 = 0
ㄴ 평균 - O(n^2)
- 레코드의 이동 과다 : 이미 정렬 위치에 있어도 교환되는 일잉 일어남. 이동연산은 비교연산보다 더 많은 시간 소요
===>> 부분적으로 정렬된 데이터셋에서 더 효율적, small datasets에 적합, stable-sort, simplicity
12.5 쉘 정렬
셀 정렬

- 삽입정렬이 어느 정도 정렬된 배열에서 대단히 빠른 것에 착안. (삽입 정렬은 이웃한 위치로만 이동하므로, 많은 이동에 의해서만 제자리 찾아감)
-> 요소들이 멀리 떨어진 위치로 이동 -> 적게 이동하여 제자리 찾을 수 있음
- 전체 리스트를 일정 간격(gap)의 부분 리스트로 나눔
==> 나뉘어진 각각의 부분 리스트를 삽입정렬
그 후 간격을 1/2 줄여서 다시. 마지막은 간격 1

셀 정렬 프로그램
//gap 만큼 떨어진 요소들을 삽입정렬
//정렬의 범위는 first에서 last
inc_insertion_sort (int list[], int first, int last, int gap)
{
int i, j, key;
for (i=first+gap; i<=last; i=i+gap) {
key = list[i];
for (j=i-gap; j>=first && key<list[j]; j=j-gap)
list[j+gap] = list[j];
list[j+gap] = key;
}
}
//
void shell_sort (int list[], int n) //n=size
{
int i, gap;
for (gap=n/2; gap>0; gap=gap/2) {
if ((gap%2)==0)
gap++;
for (i=0; i<gap; i++) //부분 리스트의 개수는 gap
inc_insertion_sort(list, i, n-1, gap);
}
}
셀 정렬 복잡도 분석
- 셀 정렬 장점 ⓛ : 불연속적인 부분 리스트에서 원거리 자료 이동으로 보다 적은 위치교환 가능성 증가 (삽입정렬은 한칸씩만 이동 ㅜ)
- 셀 정렬 장점 ② : 부분 리스트가 점진적으로 정렬된 상태가 되므로 삽입정렬 속도 증가
- 시간 복잡도 ***gap(간격)에 많은 영향
ㄴ 최악 : O(n^2)
ㄴ 평균 : O(n^1.5)
-**stable sort, in-place sort -> space complextity = O(1)
12.6 합병 정렬
합병 정렬 ( merge sort )

- 리스트를 두개의 균등한 크기로 분할하고 분할된 부분리스트를 정렬
- 정렬된 두 개의 부분 리스트를 합하여 전체 리스트를 정렬
(divide and conquer 분할 정복 기법에 바탕)

2개의 정렬된 리스트 합하는 과정
합병정렬 알고리즘
| 1. 분할 (Divide) : 배열을 같은 크기의 2개의 부분 배열로 분할 2. 정복 (Conquer) : 부분 배열을 정렬.(합병 정렬 순환 적용) 부분 배열 크기가 충분히 작지 않으면... 재귀호출로 다시 분할 정복기법 적용 3. 결합 (Combine) : 정렬된 부분배열을 하나의 배열에 통합 ( 이 단계에서 정렬 수행!! ) merge_sort(list, left, right) : 1. if left < right 2. mid = (left + right) / 2; 3. merge_sort(list, left, mid); ==> 분할 4. merge_sort(list, mid+1, right); ==> 분할 5. merge(list, left, mid, right); ==> 합병 |
합병 알고리즘
//합병 알고리즘
merge(list, left, mid, right):
//2개의 인접한 배열 list[left..mid]와 list[mid+1..right]를 합병
i<-left;
j<-mid+1;
k<-left;
sorted 배열 생성;
while i <= mid and j <= right do
if (list[i] < list[j] ) then
sorted[k]<-list[i];
k++;
i++;
else
sorted[k]<-list[j];
k++;
j++;
요소가 남아있는 부분배열을 sorted로 복사;
sorted를 list로 복사;**합병 중간 sorted 배열 C 필요. 배열 C는 임시 저장소이므로 원 배열 list[]에 copy해애 recursive call 이 제대로 수행
==>> 추가 공간 필요, not in-place , 공간 복잡도 O(n)
합병정렬 프로그램
int sorted[MAX_SIZE]; //추가 공간 필요
//i는 정렬된 왼쪽리스트에 대한 인덱스
//j는 정렬된 오른쪽리스트에 대한 인덱스
//k는 정렬될*** 리스트에 대한 인덱스
void merge(int list[], int left, int mid, int right)
{
int i,j,k,l;
i=left; j=mid+1; k=left;
while (i<=mid && j<=right) { //분할 정렬된 list의 합병
if (list[i] <= list[j]) sorted[k++] = list[i++]; //non-decreasing order -> 더 작은 것을 먼저 copy
else sorted[k++] = list[j++];
}
if (i > mid) //왼쪽 배열A는 모두 copy 되었다는 뜻
for (l=j; l<=right; l++)
sorted[k++] = list[l]; //혹시 오른쪽 배열B에 남은 것 있으면 for문 실행
else //남아 있는 레코드의 일괄 복사
for (l=i; l<=mid; l++) //혹시 왼쪽 배열A에 남은 것 있으면 for문 실행
sorted[k++] = list[l];
//배열 sorted[]의 리스트를 배열 list[]로 복사
for (l=left; l<=right; l++) //**sorted[]는 임시 저장소이므로 원 배열 list[]에 copy해야 recursive call이 제대로 수행
list[l] = sorted[l]; // |right-left|만큼의 이동 연산 -> O(n)
void merge_sort(int list[], int left, int right)
{
int mid;
if (left < right)
{
mid = (left+right)/2; //리스트의 균등분할
merge_sort(list, left, mid); //부분리스트 정렬
merge_sort(list, mid+1, right); //부분리스트 정렬
merge(list, left, mid, right); //합병
}
}**만일 record 개수가 33개인 dataset을 merge sort하면 merge() 함수는 총 몇번 호출?
recursive call 횟수는 log(n), n=dataset 크기 ( or 정렬하고자 하는 record 개수)
합병정렬 복잡도 분석
merge 함수에서 비교 연산과 이동연산이 수행되는 것.
- 비교 횟수 :
크기 n 리스트 균등분배이므로(2^3->2^2->2^1->2^0) log(n)개의 레벨 + 각 레벨에서 모든 레코드 n개 비교하므로 n번 비교 연산 ==>> 최대 nlog2(밑)의 n(지수)번 필요
- 이동 횟수 :
레코드의 이동이 각 패스에서 2n번 발생 ==> 전체 레코드 이동은 2n*log(n)번 발생
ㄴ 레코드 크기가 크면 매우 큰 시간적 낭비 / 레코드를 연결리스트로 구성하여 합병 정렬하면 매우 효율적
- 최적, 평균, 최악 모두 차이 없이 O(n*log(n))의 복잡도
- 안정적, 데이터 초기 분산 분포에 영향 ↓ ↓ ↓
- not in-place, 공간 복잡도 O(n)
12.7 퀵 정렬
퀵 정렬 ( quick sort )

- 평균적으로 가장 빠른 정렬 방법
- 분할정복법 사용
- 합병 정렬과 달리 리스트를 2개의 부분리스트로 비균등 분햘 -> 각각 부분리스트 다시 퀵정렬(재귀호출)
- **how to choose pivot? => 가능하면 선택된 pivot에 의해 얻어진 부분리스트의 길이가 비슷하도록. 즉, unsorted list 내 key들 중 중간 값
퀵 정렬 알고리즘
| void quick_sort(int list[], int left, int right) { if (left < right) { int q = partition(list, left, right); quick_sort(list, left, q-1); quick_sort(list, q+1, right); } } |
퀵 정렬 코드
int partition (int list[], int left, int right) //int q = partition(list, left, right);
{
int pivot, temp;
int low, high;
low = left;
high = right+1;
pivot = list[left]; //현 리스트의 가장 왼쪽 record의 key가 pivot
do {
do
low++;
while (low <= right && list[low] < pivot);
do
high--;
while (high >= left && list[high] > pivot);
if (low < high) SWAP(list[low], list[high], temp); //이때 high값이 pivot이 들어갈 자리이며 그 자리가 pivot 값의 최종자리!!
} while (low < high); //if high < low then NO swapping and Done!
SWAP(list[left], list[high], temp; //pivot(list[left])을 정렬된 자리로~!
return high; //pivot이 정렬된 index를 반환
}
void quick_sort(int list[], int left, int right)
{
if (left < right)
{
int q = partition(list, left, right);
quick_sort(list, left, q-1);
quick_sort(list, q+1, right);
}
}
int main(void)
{
int i;
n = MAX_SIZE;
srand(time(NULL));
for (i=0; i<n; i++) //난수 생성 및 출력
list[i] = rand()%100;
quick_sort(list, 0, n-1) //퀵 정렬 호출
for (i=0; i<n; i++)
printf("%d", list[i]);
printf("\n");
return 0;
}실행결과 : 16 24 25 38 49 64 87 90 93 96
퀵 정렬 복잡도 분석
- 최선 (거의 균등한 리스트로 분할한다고 가정)
ㄴ 패스 수 : log(n)
ㄴ 각 레벨에서 비교횟수: n
ㄴ 총 비교횟수 : n*log(n)
ㄴ 총 이동횟수 : 비교횟수에 비해 적으므로 무시 가능
ㄴ **만일 pivot을 잘 정해서 두 sub list가 유사한 크기로 분할되면 quick_sort() 함수의 총 호출횟수는 O(logn)
- 최악 (극도로 불균등한 리스트로 분할)
ㄴ 레벨 수 : n
ㄴ 각 레벨 안 비교횟수: n
ㄴ 총 비교횟수 : n^2
ㄴ 총 이동횟수 : 무시 가능
ㄴ **만일 pivot을 잘못 정해서 항상 두 sub list 중 하나의 크기가 1이면 quick_sort() 함수의 총 호출횟수는 O(n)
- 중간값을 피벗으로 선택하면 불균등 분할 완화 가능
- 한번 선택된 pivot은 최종 자리 찾고 아후, 연산에서 배제
- 불필요한 데이터 이동 줄임 (fast and no extra memory needed)
-**fast, no extra memory needed, in-place sort algorithm
12.9 기수정렬
기수정렬 (Radix Sort)

- 대부분의 정렬 방법들은 레코드들을 비교함으로써 정렬 수행
- but 기수 정렬은 레코드를 비교하지 않고 정렬 수행
(비교 연산 전혀 사용하지 않음~!)
- O(dn)의 시간복잡도 가짐
(d:key값이 숫자인 경우, 자리수)
+ 추가적인 메모리를 필요
기수(radix) : 숫자의 자리수 (단계의 수는 자리수의 개수와 일치)
- 한자리수 기수정렬 : 단순히 자리수에 따라 버켓에 넣었다가 꺼내면 정렬
- 두자리수 기수정렬 : 낮은 자리수로 먼저 분류한 다음 다시 높은 자리수로 분류
***추가 공간 필요. not in-place
기수정렬 알고리즘
| RadixSort(list, n): 1. for d<-LSD의 위치 to MSD의 위치 do { 2. d번째 자리수에 따라 0번부터 9번 버켓에 넣는다 3. 버켓에서 숫자들을 순차적으로 읽어서 하나의 리스트로 합친다 4. d++; 5. } //LSD (Least Significant Digit) 가장 낮은 자리수 <-> MSD (Most) |
- 버켓은 큐로 구현 (먼저 들어간 숫자들이 먼저 나와야 함)
- 버켓의 개수는 키의 표현 방법과 밀접한 관계 (알파벳문자면 버켓 26개)
- 패스의 개수는 자리 개수(d)에 밀접한 관계
기수정렬 프로그램
//6장의 큐 소스를 여기에...
#define BUCKETS 10 //한 자리가 0~9까지 10가지로 표현되므로 bucket 수는 10
#define DIGITS 4 //key가 4자리 수
void radix_sort(int list[], int n)
{
int i, b, d, factor=1;
QueueType queues[BUCKETS];
for (b=0; b<BUCKETS; b++) //bucket만큼의 큐들의 초기화
init(&queues[b]); //큐들의 초기화
for (d=0; d<DIGITS; d++) { //낮은 자리수부터 정렬!
for (i=0; i<n; i++) //전체(n) 데이터들을 자리수에 따라 큐에 입력
enqueue(&queues[(list[i]/factor) % 10], list[i]); //%10은 끝자리 반환
for (b=i=0; b<BUCKETS; b++) //버켓에서 꺼내어 list로 합침
while (!is_empty(&queues[b]))
list[i++] = dequeue(&queues[b]); //한 패스 정렬됨
factor *= 10; //그 다음 자리수로 간다 d가 +1 => factor는 X10
} //(outer for)d번 반복 X (inner for)n번 반복 => O(dn)
}
//define SIZE 10
int main(void)
{
int list[SIZE];
srand(time(NULL));
for (int i=0; i<SIZE; i++) //난수 생성 및 출력
list[i] = rand()%100;
radix_sort(list, SIZE); //기수정렬 호출
for (int i=0; i<SIZE; i++)
printf("%d", list[i]);
printf("\n");
return 0;
}실행 결과: 22 38 71 76 81 83 89 94 97 98
기수정렬 복잡도 분석
- n개의 레코드, d개의 자릿수로 이루어진 키를 기수 정렬할 경우
ㄴ 메인 루프는 자릿수 d번 반복 / 큐에 n개의 레코드 입력 수행
- O(dn)의 시간적 복잡도 (d는 아주 작아서 O(n)이라고 해도 됨)
ㄴ 키의 자릿수 d는 10이하의 작은 수이므로 빠른 정렬
(실수, 한글, 한자로 이루어진 키는 정렬X 숫자만 가능)
***not in-place
12.10 정렬 알고리즘 비교

정렬 알고리즘들의 복잡도 비교
13.1 탐색이란?
13.2 정렬되지 않은 배열에서의 탐색
13.3 정렬된 배열에서의 탐색
13.4 이진 탐색 트리
13.5 AVL 트리
13.6 2-3 트리
13.7 2-3-4 트리
13.1 탐색이란?
탐색
- 여러 개의 자료 중에서 원하는 자료를 찾는 작업
- 탐색용 자료구조: 배열, 연결리스트, 트리, 그래프
- 탐색키 (search key): 항목과 항목 구별해주는 키
13.2 정렬되지 않은 배열에서의 탐색
순차탐색 (sequential search)
- 가장 간단, 직접적 탐색 방법
- 정렬x sequence을 처음부터 마지막까지 하나씩 검사하는 방법
- 평균 비교 횟수 : 탐색 성공 => (1+2+...+n)/n = (n+1)/2번 비교 / 탐색 실패 => n번 비교 ==>> O(n)
- 시간 복잡도
최선 : 찾는 것이 가장 앞 O(1)
최악 : 찾는 것이 가장 뒤 O(n)
평균 : (탐색 성공시 비교횟수 모두 더한것) / (n+1) < O(n)
순차 탐색 프로그램
int seq_search(int key, int low, int high) //record 개수 = (high-low+1) = n
{
int i;
for (i=low; i<=high; i++) //for 문 안의 비교를 제거 => 그래도 여전히 최악의 경우 n번 반복 O(n)
if (list[i] == key)
return i; // 탐색 성공하면 키 값의 인덱스 반환
return -1;
}
//개선된 순차탐색
int seq_search2(int key, int low, int high)
{
int i;
list[high + 1] = key; //키 값을 찾으면 종료
for (i=low; list[i] != key; i++);
if (i == (high+1)) return -1; 탐색 실패
else return i; // 탐색 성공
}
13.3 정렬된 배열에서의 탐색
정렬된 배열을 이용한 이진탐색 (binary search)
- 정렬된 배열의 (그래서 고정된 dataset이 적절) 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 배열에 있는지를 알아내어 탐색 범위를 반으로 줄인 탐색 진행
이진탐색 알고리즘
| search_binary(list, low, high): 1. middle <- low에서 high사이의 중간 위치 2. if (탐색값 == list[middle]) 3. return middle; //탐색성공은 여기서!! 4. else if (탐색값 < list[middle]) 5. return list[low]부터 list[middle-1]에서 탐색; 6. else if (탐색값 > list[middle]) 7. return list[middle+1]부터 list[high]에서 탐색; |
순환 호출 버전 이진탐색 코드
//순환을 이용한 이진탐색 프로그램
int search_binary1(int key, int low, int high)
{
int middle;
if (low <= high) { //종료조건(실패 판단조건)
middle = (low + high)/2;
if (key==list[middle]) //탐색 성공
return middle; //탐색성공은 여기서!!
else if (key < list[middle]) //왼쪽 부분리스트 탐색
return search_binary1(key, low, middle-1);
else //오른쪽 부분리스트 탐색
return search_binary1(key, middle+1, high);
} //탐색 실패
return -1;
}
반복적인 버전 이진탐색 코드
int search_binary2(int key, int low, int high)
{
int middle;
while (low <= high) { //아직 숫자들이 남아 있으면
middle = (low + high) / 2;
if (key == list[middle])
return middle;
else if (key > list[middle])
low = middle + 1;
else
high = middle - 1;
}
return -1; //발견되지 않음
}순환 이진탐색 프로그램 => 탐색범위가 n -> n/2 -> n/2^2 -> n/2^4 -> ... 1 로 줄어듬 => O(logn) 밑 2
반복 이진탐색 프로그램 => 탐색범위가 n -> n/2 -> n/2^2 -> n/2^4 -> ... 1 로 줄어듬 => O(logn) 밑 2
**이론적 시간복잡도는 둘이 동일하나, Call stack 을 이용한 context switching, push/pop이 없는 반복 호출 방법이 더 빠름
색인 순차탐색 (indexed sequential search)

- 인덱스 테이블 사용하여 탐색 효율 증대
-> 주자료 리스트에서 일정 간격으로 발췌한 자료 저장
- 복잡도 : O((m+n)/m) => 인덱스 테이블의 크기 m, 주자료 리스트의 크기 n
색인 순차 탐색 코드
#define INDEX_SIZE 256
typedef struct
{
int key;
int index;
} itable;
itable index_list[INDEX_SIZE];
//INDEX_SIZE는 인덱스 테이블의 크기, n은 전체 데이터의 수
int search_index(int key, int n)
{
int i, low, high;
//키 값이 리스트 범위 내의 값이 아니면 탐색 종료
if (key<list[0] || key>list[n-1])
return -1;
//인덱스 테이블을 조사하여 해당키의 구간 결정
for ( i=0; i<INDEX_SIZE; i++)
if (index_list[i].key <= key && index_list[i+1].key>key)
break;
if (i==INDEX_SIZE) { //인덱스 테이블의 끝이면
low = index_list[i-1].index;
high = n;
}
else {
low = index_list[i].index;
high = index_list[i+1].index;
}
//예상되는 범위만 순차 탐색
return seq_search(key, low, high);
}
정렬된 배열을 이용한 보간탐색 (interpolation search)
- 사전이나 전화번호부 탐색하는 방법
- 탐색키가 존재할 위치를 예측하여 탐색 => O(log(n)) (밑 2)
- 보간 탐색은 이진 탐색과 유사 but 리스트를 불균등 분할하여 탐색 (데이터 값이 비교적 균등하면 이진탐색보다 빠름)
ps. 이진 탐색에서 탐색 위치는 항상 (low + high)/2

보간탐색 위치 예측 수식
보간탐색 코드
int interpol_search(int key, int n)
{
int low, high, j;
low = 0;
high = n-1; while(low <= high) {
while ((list[high] >= key) && (key > list[low])) {
j = ((float)(key-list[low]) / (list[high]-list[low])*(high-low))+low; //O(log(n)) while문 한번 실행 후 list[]의 크기가 /x (<=2)로 줄어듬.
if (key>list[j]) low=j+1;
else if (key<list[j]) high=j-1;
else return j; //탐색성공
}
return -1; //탐색실패
}주의 : 만약 나눗셈 계산할 때 float로 형변환 안해주면 정수로 계산돼서 항상 0이 됨
13.4 이진 탐색 트리
이진탐색트리 (BST: Binary Search Tree)
- 이진탐색과 이진탐색트리는 근복적으로 같은 원리에 의한 탐색 구조
- 이진탐색은 자료들이 배열에 저장되어 있어 삽입/삭제 매우 비효율 but 이진탐색 트리는 빠르게 삽입/삭제 수행

따라서 이진 탐색 트리에서는 최악을 피하기 위해 균형을 유지하는 것이 무엇보다 중요!
균형 이진탐색트리 (Balanced BST)
- 이진탐색트리에서의 시간복잡도 ***이진탐색트리를 이용한 모든 연산의 time complexity는 O(h) (h=트리 높이 logn or n)
ㄴ 균형트리 : O(log(n))
ㄴ 불균형트리 : O(n), 순차탐색과 동일
***탐색 작업 효율적으로 하기 위해 중위순회하면 오름차순으로 정렬된 값 얻음
==>> key(왼쪽서브트리) < key(루트노드) < key(오른쪽서브트리)
13.5 AVL 트리
AVL 트리
- 모든 노드의 왼쪽과 오른쪽 서브트리의 높이 차가 1이하인 이진탐색트리
- 트리가 비균형 상태로 되면 스스로 노드들을 재배치하여 균형 상태 유지
- 시간복잡도
ㄴ 평균, 최선 최악 모두 : O(log(n))
- 균형 인수 (balace factor) = 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
- 모든 노드의 균형인수가 ±1 이하면 AVL 트리
AVL 트리의 연산
- 탐색 연산 : 이진탐색트리와 동일 O(logn) (밑2)
- 삽입 위치에서 루트까지의 경로에 있는 조상 노드들의 균형 인수 영향
- 삽입 후에 불균형 상태로 변한 가장 가까운 조상 노드(균형 인 수가 ±2가 된 가장 가까운 조상 노드)의 서브 트리들에 대하 여 다시 재균형
- 삽입 노드부터 균형 인수가 ±2가 된 가장 가까운 조상 노드까지 회전
***AVT 트리 마지막 완성된 트리 그리시오 문제 냈다. => 고치는것까지 할 수 있어야.

AVL트리 삽입시 균형 깨지는 4가지 경우
- in-order로 읽으면 됨
그림보고 => 어디다 붙일지 알아야함
J: 새로 삽입된 노드
X: 노드 J와 가장 가까우면서 균형 인수가 ±2가 된 조상 노드

AVL 트리 구축 예시
AVL 트리 구현 코드
#include <stdio.h>
#include <stdlib.h>
//AVL 트리 노드 정의
typedef struct AVLNode
{
int key;
struct AVLNode *left;
struct AVLNode *right;
} AVLNode;
//노드 동적 생성 함수
AVL_Node* create_node(int key)
{
AVLNode* node = (AVLNode*)malloc(sizeof(AVLNode));
node->key = key;
node->left = NULL;
node->right = NULL;
return(node)
}
//오른쪽으로 회전시키는 함수
AVLNode *rotate_right(AVLNode *parent)
{
AVLNode* child = parent->left;
parent->left = chile->right;
chile->right = parent;
//새로운 루트를 반환
return child;
}
//왼쪽으로 회전시키는 함수
AVLNode *rotate_left(AVLNode *parent)
{
AVLNode* child = parent->left;
parent->right = chile->left;
chile->left = parent;
//새로운 루트를 반환
return child;
}
//트리의 높이를 반환
int get_height(AVLNode *node)
{
int height = 0;
if (node != NULL)
height = 1 + max(get_height(node->left),
get_height(node->right));
return height;
}
//노드의 균형인수 반환
int get_balance(AVLNode* node)
{
if (node == NULL) return 0;
return get_height(node->left) - get_height(node->right);
}

실행결과 :
전위 순회 결과
[30] [20] [10] [29] [40] [50]
13.6 2-3 트리
2-3 트리
- 차수(자식노드 개수)가 2 또는 3인 노드를 가지는 트리 (중복키 허용X)
- 2-노드
- 이진탐색트리와 유사
- 나의 데이터 k1와 두개의 자식 노드 가짐
- 왼쪽 서브 티리에 있는 데이터들은 모두 k1보다 작은 값
- 중간 서브 트리에 있는 값들은 모두 k1 보다 크고 k2보다 작다 ?오타인가 ??
- 3-노드
- 2개의 데이터 (k1,k2)와 3개의 자식노드 가짐
- 왼쪽 서브 트리에 있는 데이터들은 모두 k1보다 작은 값
- 중간 서브 트리에 있는 값들은 모두 k1보다 크고 k2보다 작다
- 오른쪽에 있는 데이터들은 모두 k2보다 크다


단말노드 분리의 경우

비단말 노드 분리의 경우

루트 노드 분리의 경우
2-3 트리 탐색 프로그램
tree23_search(Tree23Node *root, int key)
{
if (root == NULL) // 트리가 비어 있으면
return FALSE;
else if (key == root->key1) // 루트의 키==탐색 키
return TRUE;
else if (root->type == TWO_NODE) { // 2-노드
if (key < root->key1)
return tree23_search(root->left, key)
else
return tree23_search(root->right, key)
} else { // 3-노드
if (key < root->key1)
return tree23_search(root->left, key)
else if (key > root->key2)
return tree23_search(root->right, key)
else
return tree23_search(root->middle, key)
}
}
'Study > Data Structure' 카테고리의 다른 글
| [자료구조 스터디] chap.13 탐색 (0) | 2023.12.01 |
|---|---|
| [자료구조 스터디] chap.12 정렬 (0) | 2023.11.21 |
| [자료구조 스터디] chap.10 그래프 I (0) | 2023.11.20 |
| [자료구조 스터디] chap.11 그래프 II (0) | 2023.11.16 |



